GIS Datasets for Climate and Heat

I presented a poster last April on the library’s GIS and Data Services at the CHAIRS-C conference at the Brown School of Public Health. CHAIRS-C is an acronym for Center on Heat, Health, and Aging Innovation and Research Solutions for Communities; it’s a small cluster whose members are interested in heat-related research, and the impact of extreme heat on vulnerable communities. I provided some examples in the poster of heat-related datasets and research that I’ve supported over the last few years. I thought I’d share a summary of these datasets in this post that include air conditioning, heat indices, and sources that provide climate-related rasters with variable that include temperature and precipitation. Most of these examples are US-based, the last one is global.

Local Air Conditioning Estimates (LACE)

The Local Air Conditioning Estimates (LACE) is a new, experimental dataset produced by the US Census Bureau. It includes estimates of occupied housing units that have air conditioning at the national, state, county, and census tract levels. The estimates are published with margins of error at a 90% confidence level, and represent the year 2023. Each record includes the census summary level / fips GEOID, so you can readily match them to vector boundary files for GIS mapping.

Census AC data spreadsheet — Sample records from the Local Air Conditioning Estimates for census tracts

Questions about air conditioning are regularly collected as part of the American Housing Survey (AHS), but the sample size isn’t large enough to publish reliable estimates below the state and metropolitan area levels. To create LACE, the Census Bureau employed machine learning in a process called cross survey modeling, and triangulated the AHS with some other datasets to create small-area estimates. Summary documentation is included on the LACE website if you want to learn more, and there are links to working papers that go into greater detail.

The concept is similar to what the CDC has done in taking data from the Behavioral Risk Factor Surveillance System and using models to create small area estimates for the PLACES project. LACE fills a vital data gap for studying heat; most small-area sources for AC are a patchwork series of parcel data published by individual municipalities. I attended a couple of presentations given by the Census Bureau at FedGeoDay back in April, and they suggested that they will increasingly move in a modeling direction that draws on administrative data and smaller surveys, given declining response rates to large sample surveys like the ACS. Of course, this was before the current administration made the bonkers decision to ban the use of injecting noise into statistical datasets (a basic practice for protecting the privacy of survey participants), so who knows what will happen next.

Urban Heat Severity Index

Research has shown that temperature varies considerably over small areas, especially in cities. So if you are looking at the temperature reported for an entire city, or even at gridded data where the cells are large, both will mask a good deal of geographic variability. The absence of trees and green space, an abundance of impervious surfaces, and concentrated emissions from vehicles and air conditioners can dramatically increase the temperature of urban areas, creating “heat islands”.

The Trust for Public Land has been publishing the annual Heat Severity Urban Areas index for the past few years; originally the dataset covered just incorporated places but was expanded to include the entire US. Index values from 1 to 5 indicate the severity of a heat island, measured relative to the average summer temperature for the city or place where each grid cell is located. The data is published as a grid at 30m resolution (matching the resolution of LANDSAT imagery used in their workflow) and is distributed via an ESRI hub site. You can search for it within the Living Atlas in the data catalog in ArcGIS Pro to add it to a project, or grab the url from the hub site to render it as a web mapping service in QGIS or another package. In order to use it in an analysis, you’ll need to export and save the raster locally. To save time and space, you can clip the layer to a polygon or extent of the screen, and then save the result.

For one project, I had to estimate the number of people in Rhode Island who were living within an urban heat island. I used census block boundaries from the 2020 census, which include total population and housing units as attributes, calculated the centroid of the blocks, and overlaid them on the grid and assigned the intersecting grid value to each point. Then I summed the population by the index values; a value of null indicated that the center of the block fell outside a heat cell.

Urban Heat Severity Index in Providence with census blocks — Urban Heat Severity Index overlayed with census blocks in Providence, RI in ArcGIS Pro

US Gridded Climate Data: PRISM

For rasters of climate data on temperature and precipitation, I’ve often turned to PRISM at Oregon State University. They work with the USDA to generate the maps for plant hardiness zones, and have developed a model to generate gridded climate data. The public data is available at 4km resolution, but researchers with project proposals can submit requests to access 800m resolution data. They publish mean daily, monthly, and annual values, as well as normals. Each raster is stored in one file, where the file represents one observation for one time period. I have written about PRISM in the past as I used it for several projects, writing Python scripts to pull a raster file for specific dates that match attributes in a point file, in order to determine what the temperature was for that date for each point, based on the grid cell the point fell within. PRISM has updated some of their products since I’ve run that analysis, specifically replacing the older raster file formats with tifs.

US County Climate Data: NCEI Climate at a Glance

For certain statistical analyses, it can be helpful to have climate data summarized for an entire geographic area so that it aligns with other variables that are published for that area. NOAA’s National Center for Environmental Information (NCEI) employs a model that takes their gridded data product (derived from the U.S. Climate Divisional Database) to produce monthly state and county-level estimates for the US, from 1895 to the present. I wrote a post that summarizes how to download, interpret, and parse these files so that you can start using them; if you’re seeking the entire dataset you’ll skip the web-based interface for creating summary charts and maps and go right to the FTP site to download data in bulk.

Since our current government doesn’t like the weather, this is one of the datasets that I’ve archived in DataLumos as part of the Data Rescue Project, in case it vanishes one day.

NOAA NCEI county average temperature map

Global Climate Data: ERA5

How about the rest of the world? ERA5 is produced by the European Centre for Medium-Range Weather Forecasts, which publishes gridded climate data at 1/4 degree resolution, modeled from 1940 to present. You can choose hourly, daily, or monthly estimates (accessed via separate web pages), and at the download stage you can provide bounding box coordinates to clip the data (so you don’t have to download the entire planet). The data is packaged in a GRIB file, where variables are stored in separate bands. So if you download monthly data for one variable, each month is stored sequentially; if you download two or more variables, they are sorted by variable and then by time period. Similar to my US project with PRISM, I wrote a Python script that extracts ERA5’s monthly gridded data for specific point locations, but in this case I pulled all dates for each point (with an option to highlight a specific month for a matching date). I wrote a detailed post that describes the dataset and process.

ERA5 temperature data in QGIS — ERA5 mean monthly temperature data for Sierra Leone in QGIS

Talks and Travels: Conferences and the Camino

I haven’t been keeping up with posting, as these past few months have been atypical. April was devoted to attending conferences and giving presentations. Much of this was prompted by my recent work with the Data Rescue Project, and the HIFLD Open rescue initiative in particular. The month began with a panel at Brown’s Data Science Institute, where the topic was Trust in Data. A few days later, I joined local colleagues at the Northeast Higher Ed GIS Facilitators Meet Up in Worcester, MA. I was honored to serve as the keynote speaker for the annual Big 10 GIS Conference (held virtually), where I presented on preserving federal datasets and the HIFLD Open rescue initiative. Shortly thereafter, I traveled to the Census Bureau’s headquarters just outside of DC for FedGeoDay 2026 and served on a panel of non-federal data providers who are contributing to the national data ecosystems. I came back to Providence just in time to give a poster presentation on our GIS and Data Services at the CHAIRS-C conference (Center on Heat, Health, and Aging Innovation and Research Solutions for Communities at the Brown University School of Public Health).

Then in May, I went off the grid. My wife and I traveled to Northwestern Spain to walk the Camino de Santiago, or Way of St. James. Established in the Middle Ages, the Camino is a series of routes that drew Christian pilgrims from throughout Europe to the Cathedral in Santiago de Compestella, which is believed to be the resting place of the apostle St James, brother of St John. We walked the Camino Primitivo, which is the “original” route established by King Alfonso II circa 814 AD. It’s also considered to be the most challenging of the routes, as it climbs through mountains and forests before descending into farmland. It’s not considered a “wilderness” hike however, as all of the routes follow a mix of unpaved and paved roads between towns and villages. A map of the primary routes (from Wikipedia) is below. The French Way is considered the primary route and is the most heavily traveled. The Portuguese and Northern Ways are also popular, followed by the Primitivo.

Map of the Primary Camino Routes — By WikiPate – credit to Sémhur, and for the logo: Manfred Zentgraf, CC BY-SA 4.0, Map from Wikimedia

The paths are marked at regular intervals, and whenever you have to turn or change direction. You look for a white or grey stone marker with a scallop shell, a symbol of St. James and of the Camino, to guide you. In places where a marker stone isn’t feasible, a blue and yellow tile of the shell is embedded in a wall or building to point the way. The system was so good that we rarely needed our phones; we used nothing more than our eyes and an excellent guidebook with detailed topographic maps of each stage of the journey, elevation diagrams, and a directory of landmarks and places to stay (the Village to Village Camino Guides – highly recommended).

The routes run into the hundreds of kilometers; the Primitivo is a shorter trek that covers about 320 km between Oviedo and Santiago, but in exchange for the shorter distances you have greater changes in elevation. As this was our first attempt at something like this, we opted to do half the route, beginning in a town called Grandas de Salime, located at a large dam and reservoir as you leave the region of Asturias and enter Galicia.

Our starting point: view of the Embalse de Salime from the Hotel Las Grandas

Accommodations and cafes serve pilgrims throughout the route; albergues offer a mix of hostel-like rooms (bunk beds in shared rooms) and single rooms, and there are also basic hotels. Our 183 km walk took us 9 days (3 days walking / 1 rest day in Lugo / 5 days walking). You are issued a pilgrim’s credential or passport when you begin, which grants you access to pilgrim-reserved accommodations and resources. On your journey, you need to get your passport stamped twice a day to verify that you are doing the walk. You always get a stamp at the places you stay, and in-between you can pick up others at cafes and restaurants, churches, museums, visitor centers, and even certain stores (we managed to get one at a cheese shop). Once you reach the cathedral in Santiago, you visit the pilgrim’s office (essentially the Camino DMV), where you present your passport to receive the Compostella, the official document that certifies that you finished the pilgrimage. You need to walk 100km minimum (200km if you’re biking) to qualify.

Camino Passport Stamps — A Selection of Stamps from my Pilgrim’s Credential or Passport

It was a deeply moving experience, retracing the steps that countless pilgrims took over a thousand years, and ending in front of the statue and tomb of St James behind the high altar in the cathedral, receiving the Eucharist at the Pilgrim’s mass. It was a relief to disconnect from technology and work, boiling life down to the singular goal of getting from point A to B each day. It was physically satisfying, pushing my body to walk 10 to 20 miles a day in rough terrain in all kinds of weather. It was wonderful to meet new friends; there is a cohort of people who happen to begin their journey simultaneously with you, and you see them throughout the walk, sharing the road for a time or a meal at the end of the day at the albergue. And it was a lot of fun, for a geographer who enjoys navigating a landscape with no digital do-dads, and who loves collecting stamps!

An experience like this alters your perspective, and it’s been difficult to transition back to my normal routines. It has strengthened my belief that it’s time for me to consider new possibilities and next stages in my career. Please reach out (via LinkedIn or email in the sidebar) to share opportunities. My resume is available on the About page.

Stay tuned for some heat and climate-related dataset suggestions in my next post; resources I compiled for the heat conference, and new ones I’ve learned about at FedGeoDay.

HIFLD Next GIS Data Catalog

Last December, the Data Rescue Project (DRP) finished an initiative to download and archive over 400 geospatial data layers from the defunct HIFLD Open repository to DataLumos, an ICPSR-sponsored repository for federal government datasets. I wrote this brief post that summarized our work.

The Public Environmental Data Partners and Fulton Ring have launched a new community-shaped hub for finding, previewing and downloading GIS data collections, and its debut HIFLD Next collection is built on this rescued dataset. The portal increases the accessibility of the HIFLD Open data, with enhanced options for searching, previewing attribute tables and layers, and downloading or streaming data in a number of different formats. Beyond publishing a website, the group is hoping to build a community of practitioners around this project to support and sustain it, and to provide updated datasets and additional collections in the future.

They are keen to solicit feedback from GIS data users, and particularly from librarians and data specialists who provide active user support and who would potentially refer to the portal as a source. After you’ve explored the portal, feel free to submit feedback via their survey.

To learn more about the project, you can read this press release from the PEDP and this announcement from the DRP. The project is likely to be a primary topic of discussion at FedGeoDay 2026, which takes place in late April in Washington DC.

Datasets from GeoData@SciLi: Libraries as Data Creators

While spending February buried under snow here in Providence, I took the opportunity to update several of the data products we create here at GeoData@SciLi. I’ll provide a summary of what we’re working on in this post. The heading for each project links to its GitHub repo, where you can access the datasets and the scripts we wrote for creating them.

My overall vision has always been that library data services should go beyond simply finding public data and purchasing data for students and faculty; we should actively engage in creating value-added products to meet the research and teaching needs of the university. With a dedication to open data, we also contribute to building a data infrastructure that benefits our local communities, and researchers around world. Creating our own projects keeps our technical skills sharp, gives us more in-depth knowledge about working with particular datasets, and exposes us to the practical processing problems our users face, which makes us better at understanding these issues and thus better able to serve them. To ensure that we can maintain and update our datasets, we automate and script as many of our processes as much as possible. The goal is not to build products, but to build processes to create products.

Ocean State Spatial Database

This is our signature product, a geodatabase of basic Rhode Island GIS and tabular data that folks can use as a foundation for building local projects. The idea is to save mappers the trouble of reinventing the wheel every time they want to do state-based research. I’ve honed this idea over a long period of time; as an graduate student at UW twenty years ago I was creating census databases for the Seattle metropolitan area that we published in WAGDA. I expanded this concept at CUNY, where we created and updated the NYC Geodatabase for many years, which included all forms of mass transit data (which wasn’t readily available at the time). For the Rhode Island version, I pivoted to include layers and attributes that would be of interest at a state-level, and was able to re-use many of the scripts and processes I built previously.

The Census TIGER files are the foundation, and we spent time creating suitably generalized base layers from them. Each layer or object is named with a prefix that categorizes and alphabetizes them in a logical order. “a” layers are areal features that represent land areas (counties, cities and towns, tracts, ZCTAs), “b” features are the actual legal boundaries for these areas (not generalized), “c” features are census data tables that can be joined to the a and b features, and “d” features consist of other points and lines (roads, water bodies, schools, hospitals, etc). The database is published in two formats: a Spatialite version for QGIS, and a file geodatabase for ArcGIS.

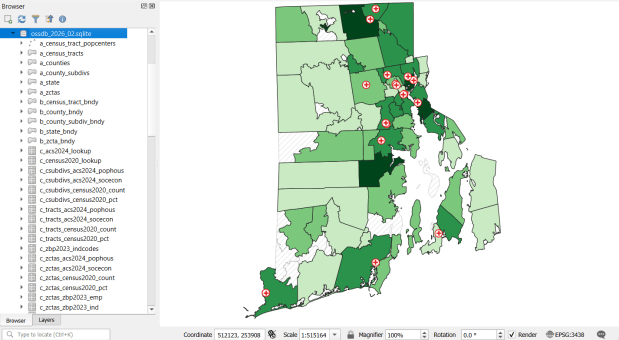
Ocean State Spatial Database Layers and Sample Map in QGIS — OSSDB Features and Sample Map in QGIS (Hospitals and the Percentage of Business Establishments that are Health Care Services by ZCTA)

Most of the features are fixed to the 2020 census and don’t change. There are two feature sets that we need to update every year. The first set are tables from the American Community Survey (ACS) and ZIP Code Business Pattern (ZBP). We’ve created tables that consist of a selection of variables that would be of broad interest to many users. We use python notebooks to download the data from the Census Bureau’s API. The ACS variable IDs and labels are stored in a spreadsheet that the script reads in, and checks it against the Census Bureau’s variable list for the demographic profile tables, to see if identifiers and labels have changed compared to the previous year. They often change, so the program flags these and we update the spreadsheet to pull the correct variables. We run the program for a specific geography, and the results are stored in a temporary database. For the ZBP data, we crosswalk and aggregate ZIP Codes to ZCTAs to create ZCTA-level data. I have separate scripts for quality control, where we check number of columns, count of rows, and any given variable to data from last year to see if there are any significant differences that could be errors, and another script for copying the data from the temporary database into the new one.

The other set of features we update are points representing schools, colleges and universities, hospitals, and public libraries. The libraries come from a federal source (IMLS PLS survey), while the others come from state sources (schools and colleges from an educational directory, and hospitals from a licensing directory). We use python to access RIDOT’s geocoding API (their parcel or point-based geocoder) to get coordinates for each feature. There’s a lot of exception handling, to deal with bad or non-matching addresses, some of which creep up every year. I store these in a JSON file; the program runs a preliminary check to see if these addresses have been corrected, and if they’re not the program uses the good address stored in the JSON. For quality control, the Detect Dataset Changes tool in the QGIS Processing toolbox allows us to see if features and attributes have changed, and we do extra work to verify the existence of records that have fallen in or out since last year.

Providence Geocoded Crime Incidents

A few years ago I had an excellent undergraduate fellow in the Data Sciences program who created a process for taking all of the police case logs from the Providence Open Data Portal and creating a GIS dataset out of them. We created this dataset for three reasons: the portal contains just the last 180 days and we wanted to create a historic archive, the records did not have coordinates, and the crimes were not standardized. Geocoding was the biggest challenge, as the location information was listed as one of the following: a street intersection, a block number, or a landmark. The script identifies the type of location, and then employs a different procedure for each. Intersections were easy, as we could pass these to the RIDOT geocoder (their street-interpolation geocoder). For block numbers, the program looks at a local file that contains all addresses in the state’s 911 database, which we filter down to just the City of Providence. It finds the matching street, gets the minimum and maximum address numbers within the given block, and computes the centroid between those addresses. For landmarks like Roger Williams Park or Providence Place Mall, we have a local list of major landmarks with coordinates that the program draws from. All non-matching addresses are written to a separate file, and you have the opportunity to add additional landmarks that didn’t match and rerun them. Crimes are matched to the FBI’s uniform categories for violent and non-violent crime, and there’s also an opportunity to update the list if new incident descriptions appear in the data.

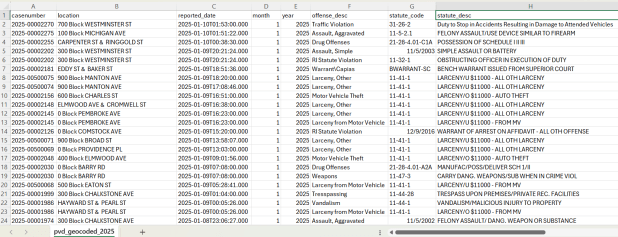
We warn users that the matches are not exact, and this needs to be kept in mind when doing any analysis; for every incident we record the match type so users can assess quality. For all of our projects, we provide detailed documentation that explains exactly how the data was created. At this point we have half the data for 2023, and everything for 2024 and 2025. We run the program a few times each year, to ensure that we capture every incident before 180 days elapses.

Providence Census Geography Crosswalk

I wrote about this project when we released it last year; it is a set of relational tables for taking census data published at the tract, block group, and block level, and apportioning and aggregating it to local Providence geographies that include neighborhoods and wards (there’s also a crosswalk for ZCTAs to local geographies, but it’s rather useless as there is little correspondence). We also published a set of reference maps for showing correspondence or lack thereof between the census and local areas.

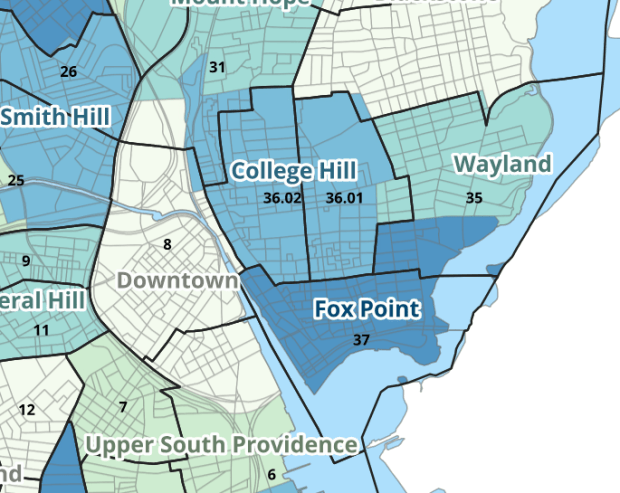
Map of Census Tracts and Neighborhoods in Providence — Census Tracts (black outlines) and Neighborhoods in Providence

The newest development is that one of my undergraduates used the crosswalk to generate 2020 census demographic profile summaries for neighborhoods and wards, so that users can simply download a pre-compiled set of data without having to do their own crosswalking. Population and household variables were apportioned using total population as a weight, while housing unit variables were apportioned using total housing units. He also generated percent totals for each variable, which required carefully scrutinizing what the proper numerators and denominators should be based on published census results. Python to the rescue again, he used a notebook that read the census tables in from the Ocean State Spatial Database, which saved us the trouble of using the census API. We publish the data tables in the same GitHub repository as the crosswalk.

UN ICSC Retail Price Indexes

I haven’t updated this one yet, but it’s next on the list. I wrote about this project a few years ago; this is a country-level index that documents variation in the cost of living at different UN duty stations. The UN publishes this data at different intervals throughout the year, in macro-driven Excel files that allow you to pull up data for one country at a time. The trick for this project was looping through hundreds of these files, finding the data hidden by the macro, and turning it into a single time series that includes unique identifiers for place, time, and good / service. This project was born from a research request from a PhD student, and we saw the value of building a process to keep it updated and to publish it for others to use. The scripting was done by the first undergraduate student worker I had at Brown, Ethan McIntosh. Thanks to him, I download the new data each year, run the program, and voila, new data!

Conclusion

I hope you found this summary useful, either because you can use these datasets, or you can learn something from one of our scripts and processes that you can apply to your own work. I hope that more academic libraries will embrace the concept of being data creators, and would incorporate this work into their data service models (along with formally contributing to existing initiatives like the Data Rescue Project or the OpenStreetMap). Feel free to reach out with comments and feedback.

Rasterio for Point Extraction of ERA5 Climate Data

I recently revisited a project from a few years ago, where I needed to extract temperature and precipitation data from a raster at specific points on specific dates. I used python to iterate through the points and pull up a raster for matching attribute dates, and Rasterio to overlay the raster and extract the climate data at those points. I was working with PRISM’s daily climate rasters for the US, where each nation-wide file represented a specific variable and date, and the date was embedded in the filename. I wrote a separate program to clip the raster to my area of interest prior to processing.

This time around, I am working with global climate data from ERA5, produced by the European Centre for Medium-Range Weather Forecasts (ECMWF). I needed to extract all monthly mean temperature and total precipitation values for a series of points within a range of years. Each point also had a specific date associated with it, and I had to store the month / year in which that date fell in a dedicated column. The ERA5 data is packaged in a single GRIB file, where each observation is stored in sequential bands. So if you download two full years worth of data, band 1 would contain January of year 1, while band 24 holds December of year 2. This process was going to be a bit simpler than my previous project, with a few new things to learn.

I’ll walk through the code; you can find the script with sample data in my GitHub repo.

There are multiple versions of ERA5; I was using the monthly averages but you can also get daily and hourly versions. The cell resolution was 1/4 of a degree, and the CRS is WGS 84. When downloading the data, you have the option to grab multiple variables at once, so you could combine temperature and precipitation in one raster and they’d be stored in sequence (all temperature values first, all precipitation values second). To make the process a little more predictable, I opted for two downloads and stored the variables in separate files. The download interface gives you the option to clip the global image to bounding coordinates, which is quite convenient and saves you some extra work. This project is in Sierra Leone in Africa, and I eyeballed a web map to get appropriate bounds.

I follow my standard approach, creating separate input and output folders for storing the data, and placing variables that need to be modified prior to execution at the top of the script. The point file can be a geopackage or shapefile in the WGS 84 CRS, and we specify which raster to read and mark whether it’s temperature or precipitation. The point file must have three variables: a unique ID, a label of some kind, and a date. We store the date of the first observation in the raster as a separate variable, and create a boolean variable where we specify the format of the date in the point file; standard_date is True if the date is stored as YYYY-MM-DD or False if it’s DD-MM-YYYY.

import os,csv,sys,rasterio
import numpy as np
import matplotlib.pyplot as plt
import geopandas as gpd
from rasterio.plot import show
from rasterio.crs import CRS
from datetime import datetime as dt
from datetime import date

""" VARIABLES - MUST UPDATE THESE VALUES """

# Point file, raster file, name of the variable in the raster
point_file='test_points.gpkg'
raster_file='temp_2018_2025_sl.grib'
varname='temp' # 'temp' or 'precip'

# Column names in point file that contain: unique ID, name, and date
obnum='OBS_NUM'
obname='OBS_NAME'
obdate='OBS_DATE'

 #The first period in the ERA data write as YYYY-MM 
startdate='2018-01' # YYYY-MM

# True means dates in point file are YYYY-MM-DD, False means DD-MM-YYYY
standard_date=False # True or False

I wrote a function to convert the units of the raster’s temperature (Kelvin to Celsius) and precipitation (meters to millimeters) values. We establish all the paths for reading and writing files, and read the point file into a Geopandas geodataframe (see my earlier post for a basic Geopandas introduction). If the column with the unique identifier is not unique, we bail out of the program. We do likewise if the variable name is incorrect.

""" MAIN PROGRAM """

def convert_units(varname,value):
    # Convert temperature from Kelvin to Celsius
    if varname=='temp':
        newval=value-272.15
    # Convert precipitation from meters to millimeters
    elif varname=='precip':
        newval=value*1000
    else:
        newval=value
    return newval

# Estabish paths, read files
yearmonth=np.datetime64(startdate)
point_path=os.path.join('input',point_file)
raster_path=os.path.join('input',raster_file)
outfolder='output'
if not os.path.exists(outfolder):
    os.makedirs(outfolder)
point_data = gpd.read_file(point_path)

# Conditions for exiting the program
if point_data[obnum].is_unique is True:
    pass
else:
    print('\n FAIL: unique ID column in the input file contains duplicate values, cannot proceed.')
    sys.exit()
    
if varname in ('temp','precip'):
    pass
else:
    print('\n FAIL: variable name must be set to either "temp" or "precip"')
    sys.exit()

We’re going to use Rasterio to pull the climate value from the raster row and column that each point intersects. Since each band has an identical structure, we only need to find the matching row and column once, and then we can apply it for each band. We create a dictionary to hold our results, open the raster, and iterate through the points, getting the X and Y coordinates from each point and using them to look up the row and column. We add a record to our result dictionary, where the key is the unique ID of the point, and the value is another dictionary with several key / value pairs (observation name, observation date, raster row, and raster column).

# Dictionary holds results, key is unique ID from point file, value is
# another dictionary with column and observation names as keys
result_dict={}  

# Identify and save the raster row and column for each point
with rasterio.open(raster_path,'r+') as raster:
    raster.crs = CRS.from_epsg(4326)
    for idx in point_data.index:
        xcoord=point_data['geometry'][idx].x
        ycoord=point_data['geometry'][idx].y
        row, col = raster.index(xcoord,ycoord)
        result_dict[point_data[obnum][idx]]={
            obname:point_data[obname][idx],
            obdate:point_data[obdate][idx],
            'RASTER_ROW':row,
            'RASTER_COL':col}

Now, we can open the raster and iterate through each band. For each band, we loop through the keys (the points) in the results dictionary and get the raster row and column number. If the row or column falls outside the raster’s bounds (i.e. the point is not in our study area), we save the year/month climate value as None. Otherwise, we obtain the climate value for that year/month (remember we hardcoded our start date at the top of the script), convert the units and save it. The year/month becomes the key with the prefix ‘YM-‘, so YM-2019-01 (this data will ultimately be stored in a table, and best practice dictates that column names should be strings and should not begin with integers). Before we move to the next band, we update our year / month value by 1 so we can proceed to the next one; Python’s timedelta function allows us to do math on dates, so if we add 1 month to 2019-12 the result is 2020-01.

# Iterate through raster bands, extract the climate value,
# store in column named for Year-Month, handle points outside the raster
with rasterio.open(raster_path,'r+') as raster:
    raster.crs = CRS.from_epsg(4326)
    for band_index in range(1, raster.count + 1):      
        for k,v in result_dict.items():
            rrow=v['RASTER_ROW']
            rcol=v['RASTER_COL']
            if any ([rrow < 0, rrow >= raster.height,
                    rcol < 0, rcol >= raster.width]):
                result_dict[k]['YM-'+str(yearmonth)]=None
            else:
                climval=raster.read(band_index)[rrow,rcol]
                climval_new=round(convert_units(varname,climval.item()),4)
                result_dict[k]['YM-'+str(yearmonth)]=climval_new
        yearmonth=yearmonth+np.timedelta64(1, 'M')

The next block identifies the year/month that matches the date for each point, and saves that value in a dedicated column. We identify whether we are using a standard date or not (specified at the top of the script). If it was not standard (DD-MM-YYYY), we convert it to standard (YYYY-MM-DD). We use the datetime function to get just the year / month from the observation date, so we can look it up in our results dictionary and pull the matching value. If our observation date falls outside the range of our raster data, we record None.

# Iterate through results, find matching climate value for the
# observation date in the point file, handle dates outside the raster       
for k,v in result_dict.items():
    if standard_date is False: # handles dd-mm-yyyy dates
        formatdate=dt.strptime(v[obdate].strip(),'%m/%d/%Y').date()
        numdate=np.datetime64(formatdate)
    else:
        numdate=v[obdate] # handles yyyy-mm-dd dates
    obyrmonth='YM-'+np.datetime_as_string(numdate, unit='M').item()
    if obyrmonth in v:
        matchdate=v[obyrmonth]
    else:
        matchdate=None
    result_dict[k]['MATCH_VALUE']=matchdate

Here’s a sample of the first record in the results dictionary:

			
{0:
{'OBS_NAME': 'alfa',
 'OBS_DATE': '1/1/2019',
 'RASTER_ROW': 9,
 'RASTER_COL': 7,
 'YM-2018-01': 28.4781,
 'YM-2018-02': 29.6963,
 'YM-2018-03': 28.9622,
 ...
 'YM-2025-12': 26.6185,
 'MATCH_VALUE': 28.7401},
 }

		

The last bit writes our output. We want to use the keys in our dictionary as our header row, but they are repeated for every point and we only need them once. So we pull the first entry out of the dictionary and convert its keys to a list, and then insert the name of the observation variable as the first list element (since it doesn’t appear in our dictionary). Then we proceed to flatten our dictionary out to a list, with one record for each point. We do a quick plot of the points and the first band (just for show), and use the CSV module to write the data out. We name the output file using the variable’s name (provided at the beginning) and today’s date.

# Converts dictionary to list for output
firstkey=next(iter(result_dict))
header=list(result_dict[firstkey].keys())
header.insert(0,obnum)
result_list=[header]
for k,v in result_dict.items():
    record=[k]
    for k2, v2 in v.items():
        record.append(v2)
    result_list.append(record)
    
# Plot the points over the first raster that was processed to see visual  
with rasterio.open(raster_path,'r+') as raster:
    raster.crs = CRS.from_epsg(4326)
    fig, ax = plt.subplots(figsize=(12,12))
    point_data.plot(ax=ax, color='black')
    show((raster,1), ax=ax)

# Output results to CSV file    
today=str(date.today())
outfile=varname+'_'+today+'.csv'
outpath=os.path.join(outfolder,outfile)
with open(outpath, 'w', newline='') as writefile:
    writer=csv.writer(writefile, quoting=csv.QUOTE_MINIMAL, delimiter=',')
    writer.writerows(result_list)   

count_r=len(result_list)
count_c=len(result_list[0])  
print('\n Done, wrote {} rows with {} values for {} data to {}'.format(count_r,count_c,varname,outpath))

Here’s a sample of the CSV output:

			
OBS_NUM	OBS_NAME	OBS_DATE	RASTER_ROW	RASTER_COL	YM-2018-01	YM-2018-02	YM-2018-03
0	    alfa	    1/1/2019	9	        7	        28.4781	    29.6963	    28.9622
1	    bravo	    7/15/2021	9	        9	        27.8433	    29.1553	    28.3196

This gives us temperature; the next step would be to modify the variables at the top of the script to read in and process the precipitation raster. Geospatial python makes it super easy to automate these tasks and perform them quickly. My use of desktop GIS was limited to examining the GRIB file at the beginning so I could understand how it was structured, and creating a visualization at the end so I could verify my results (see the QGIS screenshot in the header of this post).

Script with sample data in my GitHub repo

HIFLD Open Data Archived in DataLumos

Some good news to end the year: the Data Rescue Project has finished archiving all of the GIS data layers that were in the HIFLD Open portal, which was decommissioned at the end of summer. I wrote a post for the DRP that summarized the work we did, and you can find all the layers in ICPSR’s DataLumos repository, where you can search for and download layers one by one. I also archived the index for the series and a crosswalk that DHS published for locating updated versions of the data from the individual federal agencies that created them. If you wanted to download the entire set in bulk, it can be transferred from the Brown University Library’s GLOBUS endpoint; there are instructions for doing this on our library’s Data Rescue GitHub repo.

This project was an archival one, in that we were taking a final snapshot of what was in the repository before it went offline. In the coming year, I’ll be thinking about approaches for consistently capturing updates, and there are some folks who are interested in creating a community-driven portal to replace the defunct government site. Stay tuned!

2025 has been a tough year. Wishing you all the best for the year to come. – Frank

DataLumos HIFLD Open Archive

At These Coordinates

Dispatches from the Geospatial Data World